Ak ste nečítali predchádzajúce časti, nájdete ich tu: 1. časť :: 2. časť :: 3. časť :: 4. časť :: 5. časť
Úspešne sme spolu v našom bloku zvládli prvé a zároveň najdôležitejšie prostredie v Hejného metóde – krokovanie. Už vieme, že 3 krát (-3) vlastne znamená, že Janka urobí trikrát tri kroky dozadu. A tiež vieme, že Adam musí urobiť deväť krokov dozadu, ak chce stáť na rovnakom políčku ako Janka. Z čoho nám jasne vychádza, že 3 krát (-3) = -9. A navyše vieme, že ak ešte predtým urobíme čelom vzad, tak budeme mať –(3) krát (-3), čo je to isté, ak (-3) krát (-3) a to je to isté, ako keď my s Jankou urobíme od štartu na krokovacom páse čelom vzad a potom trikrát po tri kroky dozadu a na záver čelom vzad. A Adam, ktorý stál na začiatku vedľa nás, urobí len 9 krokov dopredu a zas bude stáť vedľa nás!!! To je predsa ľahké! Takže (-3) krát (-3) je vlastne = 9!
Sme my ale šikovníci. A to sme naozaj objavili úplne sami. Len tým, že sme veľa veľa krokovali po krokovacom páse…
Cestujeme autobusom
Skôr, ako nasadneme do autobusu a budeme sa voziť po našom meste, zopakujme si tieto
RADY:
- Plne rešpektujeme autonómiu žiaka = neopravujeme chyby, ktoré žiak urobil, ale dávame mu ďalšie úlohy, ktoré mu pomôžu chybu objaviť.
- Podporujeme diskusiu medzi žiakmi.
- Najúčinnejšou pomocou je dramatizácia.
Takmer každé dieťa vie, ako prebieha jazda autobusom verejnej dopravy alebo vlakom. Ak to nevie a nikdy to nezažilo, máte práve vynikajúci dôvod skúsiť to. Lebo raz vidieť a zažiť je lepšie ako 10-krát počuť. Účinnosť samotného pochopenia a práce v prostredí autobus závisí od skúseností, ktoré dieťa v súvislosti s cestovaním autobusom má, ale aj od prostredia, v akom prebieha samotná výučba. Základnou podmienkou je už spomínaná autonómia žiaka, čo znamená, že mu nik neradí, neopravuje jeho chyby a nedáva mu časové ohraničenia. Ak nerozumie zadaniu, opakovane si ho žiaci navzájom vysvetlia. Rodič ani učiteľ mu však neradí, ako úlohu riešiť. Či už v triede alebo doma, prevažná väčšina detí je vnútorne motivovaná tieto úlohy riešiť. Silný vplyv má samotná možnosť celú úlohu si „zahrať“.
Dramatizácia celej situácie aj v tomto prostredí, podobne ako pri krokovaní, je veľmi dôležitá a nápomocná. V triede majú deti k dispozícii model autobusu – najčastejšie je to krabica, ktorú si deti samy oblepia alebo vymaľujú, a cestujúci, ktorých pokojne zahrajú panáčikovia z hry Človeče nehnevaj sa alebo iné figúrky. Ak nemáme figúrky, môžeme ich nahradiť aj vrchnáčikmi z PET fliaš.
Doma, ak si potrebuje „jazdu autobusom“ zahrať jedno dieťa, postačí nám ako pomôcka malá krabička od čaju a gombíky alebo obyčajná fazuľa.
Najmenšie deti si celú jazdu autobusom môžu zahrať samy, pričom cestujú v skupinke a samy predstavujú cestujúcich v autobuse, vystupujúcich aj nastupujúcich.
Neskôr je veľmi dôležité, aby sme celú jazdu autobusom zaznamenali aj do tabuľky. Väčšinou je tabuľka reprezentujúca jazdu autobusom už daná. Deti si ju vždy môžu zahrať buď s použitím malej krabičky na lavici, alebo s veľkým modelom autobusu v triede. 
Táto dramatizácia môže pomôcť každému dieťaťu:
- úlohu vyriešiť,
- overiť správnosť riešenia,
- nájsť si prípadnú chybu v riešení a opraviť si ju.
Ak tieto úlohy riešia dvaja alebo viac žiakov, sú obrovským obohatením didaktického potenciálu práve ich vzájomné diskusie k riešeniu. Ak je jazda autobusom fyzicky zrealizovaná, tak k chybe v podstate vôbec nemôže dôjsť. Môže sa stať, že dieťa prehliadne dôležitý fakt, ale nepríde k chybe v myslení. Keď už žiak rieši úlohy len z tabuľky, tak je situácia iná. V tomto prípade samozrejme k chybe už môže dôjsť. Ak si ju trieda všimne, opraví ju, alebo spolužiaka na ňu upozorní a on si ju opraví sám. Ak na chybu trieda nepríde, príde na rad opäť dramatizácia a učiteľ poprosí žiaka, aby jazdu podľa tabuľky odohral s modelom autobusu a cestujúcich. Tam sa chyba určite objaví. Presne tak môže rodič pomôcť svojmu dieťaťu doma s úlohou, ktorú rieši a má problém – dramatizáciou.
Úlohy, ktorými vstúpime do prostredia Autobus sú jednoduché. V každom kroku žiak vie, čo má urobiť. Pri jazde autobusom pritom pracuje dieťa s počtom ľudí, ktorí SÚ v autobusu teraz (stav), ktorí z autobusu VYSTÚPILI alebo doňho NASTÚPILI (zmena) a ktorí na danej zastávke do autobusu PRIBUDLI alebo z neho UBUDLI (porovnanie).
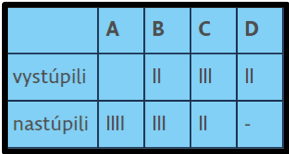Na dramatizáciu vždy vopred pripravíme aj ZASTÁVKY, na ktorých budú cestujúci nastupovať. Môžu mať mená – PRI OKNE, NA POLIČKE, KVETINKOVÁ…alebo čísla- I, II, III,…, či písmenká A, B, C… a podobne. Deti najskôr na zápis jazdy používajú vlastné záznamy, ktoré postupne vylepšujú až postupne vznikne tabuľka.
Tabuľka obsahuje všetky potrebné údaje o jazde. Deti sa učia pracovať s dátami.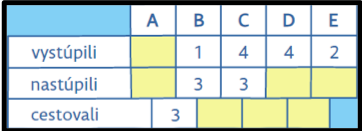 
Existuje však otázka, na ktorú im tabuľka priamu odpoveď nedá: „Koľko cestujúcich cestovalo zo zastávky A na zastávku B?“ Tento údaj musí dieťa z tabuľky vyčítať a odvodiť. Výhodnejšie je však rozšíriť tabuľku o riadok „cestovali“. Aj potom však nájdeme otázky na čísla, ktoré nie sú v tabuľke uvedené priamo. Napríklad: Koľko cestujúcich prišlo na zastávku E? Na ktorej zastávke pribudlo najviac cestujúcich? A podobne.
Náročnejšie sú úlohy, kde tomu tak nie je. V niektorých úlohách je nutné pri riešení hľadať číslo z oboch koncov. V iných poznáme doplňujúcu informáciu, ako napríklad: „na každej zastávke nastúpil rovnaký počet ľudí“, alebo „na zastávke B nastúpilo do autobusu dvakrát viac ľudí ako z neho vystúpilo“ a podobne.
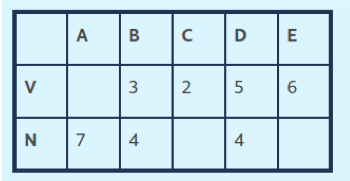Žiaci môžu pritom použiť rôzne riešiteľské stratégie ako Pokus – omyl – vylepšenie. Napríklad v nasledujúcej úlohe do prázdneho políčka napíšu číslo 2. To znamená, že z C do D cestuje 8 cestujúcich a do E by potom pricestovalo 7 cestujúcich. Zvolené číslo 2 musíme teda o jedno zmenšiť. Hľadané číslo je 1.
Niektorým dospelým sa táto riešiteľská stratégia javí ako hádanie, či prísnejšie „strieľanie od boku“. Chcú, aby žiak používal jasnú a presnú metódu. Ale pozrime sa na celú situáciu inak. V prípade uvedenej úlohy, podľa dospelého, potrebuje žiak zistiť, že na zastávku C pricestovalo 8 cestujúcich a zo zastávky C odcestovalo 7 cestujúcich a teda, že na C ubudol 1 cestujúci. Uvedená rada dospelého človeka dieťaťu je však didakticky úplne pomýlená. Predovšetkým znižuje autonómiu dieťaťa, znižuje aj jeho radosť z výsledku (áno, dá sa to tak riešiť, ale existuje oveľa lepšia metóda). Neumožňuje žiakovi získať hlboký vhľad do celej situácie v autobuse. Sú to práve chyby a ich odstraňovanie, čo tento hlboký vhľad prináša. Úplne nešťastná by bola iná rada dospelého: „Pozri, z autobusu vystúpilo celkom 16 ľudí, teda 16 tam muselo aj nastúpiť. Preto chýbajúce číslo je 1.” Najväčším prečinom takejto „rady“ je to, že dospelý ukradol dieťaťu možnosť v budúcnosti samostatne objaviť zákonitosť, ktorú mu tu práve prezradil. Už ste niekedy pozerali film s niekým, kto ho už videl a prezrádza vám dopredu, čo sa udeje v nasledujúcej chvíli? Alebo vám niekto požičal knihu a skôr ako ste ju začali čítať, vám prezradil zápletku aj rozuzlenie? Ak áno, tak viete, aké sklamanie môže prežívať dieťa, ktorému vezmete možnosť objaviť zápletku, či rozuzlenie.
Dospelý sa samozrejme môže spolupodieľať na práci dieťaťa a pomôcť mu objavovať i napredovať. Povzbudzovaním, pochvalou, ale najmä zvedavou otázkou: „Prosím ťa, ako si na to prišiel? Povedz mi to“.
Na záver dnešnej časti …
Učiteľ aj rodič musí byť predovšetkým presvedčený, že deti sú bystré a trieda pri dobrom vedení vyrieši všetky úlohy sama. O úspešnosti práce učiteľa viac ako výkony detí svedčí radosť z riešení, ktorú môžu zažívať aj slabí žiaci. Časové limity spomaľujú rozvoj matematického myslenia, pretože časť svojej intelektuálnej energie musia žiaci venovať obavám z nedodržania času. Chyby sú prítomné v každej tvorivej práci a sú dôležitým nástrojom poznania. Cez chyby človek hlbšie poznáva to, čo je predmetom jeho skúmania, v našom prípade je to evidencia jazdy autobusom. Odhaliť chybu je v našich úlohách ľahké, stačí chybne vyriešenú úlohu zahrať…
A nabudúce pokračujeme… Ak máte vy niečo, čo by ste sa radi dozvedeli, sem s tým 🙂
Miroslava Konrádová