Ak ste nečítali predchádzajúce časti, nájdete ich tu: 1. časť :: 2. časť :: 3. časť :: 4. časť :: 5. časť :: 6. časť
Autobusové linky
Zároveň so štandardným prostredím Autobus sa žiaci od prvého ročníka zoznamujú s autobusovými linkami. Tie vedú postupne k uchopeniu pojmu GRAF, pričom zastávky predstavujú uzly takého grafu a cesty medzi nimi hrany grafov. Teória grafov je však pre naše deti ešte hudbou budúcnosti. Napriek tomu je vynikajúce postupne si budovať základy jednoduchou hrou. Pamätáte si, keď ste si ako deti dávali hádanky a kreslili ste obrázky „jedným ťahom“? V jednotlivých úlohách sa pritom postupne objavujú aj otázky deliteľnosti, kombinatorické situácie a podobne.
Pracujeme s dvoma typmi liniek: Kyvadlová linka a okružná linka.
V úlohe: Na obrázku je dopravná sieť, ktorá spája obce A, B, C, D, E. Jazdí medzi nimi okružná linka 
a kyvadlová linka 
. Zisti, ako sú obce rozmiestnené.
V týchto úlohách je spočiatku skvelé dramatizovať situáciu – žiaci si môžu celú trasu „zahrať“ v škole ale aj vonku – na výlete, v družine a podobne. O pojmoch deti diskutujú a postupne získavajú vhľad do problematiky. Ak žiaci majú tendenciu rozmiestňovať obce len náhodne, je vhodné, aby im učiteľ pomáhal v premýšľaní otázkami: „Koľko je v okružnej linke obcí? Kde môže byť obec…?“ a podobne. Náročnosť úloh sa stupňuje rôznymi doplňujúcimi údajmi ako i rôznym usporiadaním obcí v sieti.
1. Objavuje sa symetria v usporiadaní siete (obr. 1):
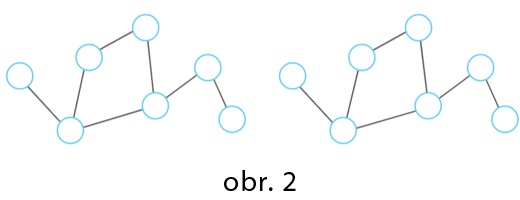
Pribúda viac obcí alebo viac liniek (obr. 2):
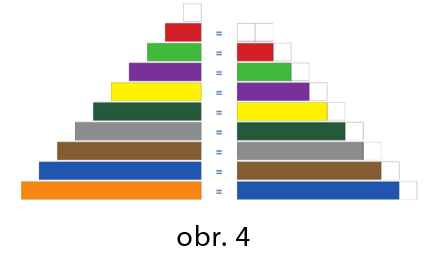
Pribúda časový údaj – počet minút medzi zastávkami (obr. 3):
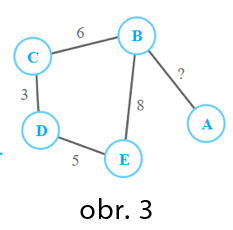
To všetko vedie postupne k objavovaniu stratégií a k rôznym kombinatorickým úvahám.
„Autobusové“ problémy vrcholia, keď žiaci sami vytvárajú harmonogram jazdy a prácou s údajmi hľadajú optimálnu trasu.
VLÁČIKY sú pomerne novým prostredím v Hejného metóde. V prostredí deti pracujú s drevenými hranolčekmi rôznych dĺžok, ktoré majú rôzne farby a rôzne dĺžky. Postupným prikladaním hranolčekov, ktoré predstavujú vagóniky vytvárame rôzne dlhé vláčiky a pracujeme s nimi. Prostredie je inšpirované tzv. Cuisenairovými hranolčekmi, ktoré sú vo svete veľmi známou pomôckou nielen v matematike. V našom prostredí sa deti hraním s vagónikmi, ich skladaním a porovnávaním učia mnohým vzťahom a pravidlám, ktoré neskôr v matematike isto zúročia.
V žiadnom prípade nie je žiadúce, aby vzťahy medzi vagónikmi a ich dĺžkami prezradil deťom nejaký „dospelák“ a tým ich ochudobnil o radosť z objavovania.
Úlohy, inak veľmi pekné a jednoduché, by sa v tom momente zmenili len obyčajným počítaním s číslami a navyše by deti prichádzali o skúsenosti, ktoré im neskôr umožnia riešiť napríklad lineárne rovnice.
Úlohy, s ktorými sa deti môžu stretnúť, sú napríklad typu:
Doplň jeden vagónik tak, aby vláčiky boli rovnako dlhé (obr. 5), či Aký vagónik je schovaný pod plachtou (obr. 6)?
Vláčiky pripomínajú prostredie Deda Lesoňa, ktoré vstupuje do učebníc v druhej triede. Podstatným rozdielom je to, že v prostredí Vláčiky deti objavujú vzťahy pomocou porovnávania a v Dedovi Lesoňovi sú tieto vzťahy dané dohodou. Dalo by sa povedať, že Vláčiky sú vynikajúcou prípravou na prostredie Dedo Lesoň, u ktorého náš dnešný výlet končí.
Dedo Lesoň je taký obyčajný rozprávkový deduško, ktorý sa na svojom dvore uprostred lesa stará o zvieratká. Po celom dvore mu behajú myšky, aby to s nimi zvládal, chová aj zopár mačiek. Keď si dokúpil aj husi, potreboval na stráženie pár psíkov. A potom si už mohol kúpiť aj niekoľko kozičiek, baranov, kráv a koní.
Tieto zvieratká si začali na dvore Deda Lesoňa porovnávať sily a odhalili niekoľko vzťahov, ktoré deti využívajú vo svojich výpočtoch. Tak ako to vlastne s tými zvieratkami je? No popravde, očami prevzdelaného dospeláka, ktorý už toho veľa zažil, vyzerá toto prostredie trochu čudne. Veď kto to kedy videl, aby sa zvieratká preťahovali lanom a zisťovali, ktoré je silnejšie? Nuž, deti milé, nedajte sa dospelákmi pomýliť… Oni sa len niekedy nevedia v matematike hrať! Ale my sa môžeme. Môžeme sa hrať na zvieratká a porovnávať ich silu v triede alebo aj vonku. Môžeme pri práci použiť ozajstné zvieratká (radšej plyšové ako živé ) alebo len kartičky s obrázkami zvieratiek. A postupne nám postačia aj symboly (staršie (obr. 7) alebo novšie (obr. 8), podľa učebnice), ktorými budeme jednotlivé zvieratká označovať.
A predstavte si to… My môžeme použiť aj ťahák! (obr. 9) V ňom vždy nájdeme, akú silu má ktoré zvieratko. No neviem, neviem, či by mu dospeláci rozumeli…
Nuž čo vy na to? Skúsime to zistiť?
Poďme sa trošku u Deda Lesoňa poobzerať. Popravde, mnoho dnešných detí už ani nevie, ako jednotlivé domáce zvieratká vyzerajú a je veľmi dobré, ak sa na návštevu pripravia ešte pred ňou tak, že sa s jednotlivými zvieratkami zoznámia. Naše spoločné skúmanie potom môžeme začať napríklad úlohami typu: Proti sebe nastúpia dve družstvá: myš a mačka oproti trom myšiam. Ktoré družstvo je silnejšie? Deti postupnou výmenou dvoch myšiek za jednu mačku, ktorá je rovnako silná získajú istotu v riešení. Uvedená operácia sa nazýva substitúcia a jej poznanie a praktické využitie prinesie dieťaťu neskôr obrovský úžitok.
Uvedenú úlohu však môžu deti vyriešiť aj inak.
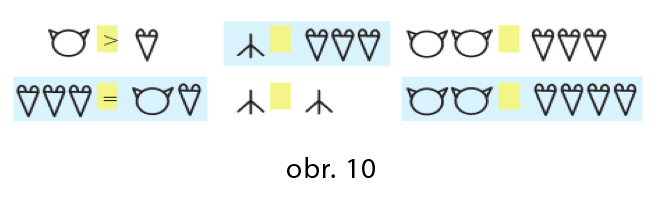
Zvieratká sa v prostredí objavujú postupne rovnako ako v našom príbehu. Do konca druhého ročníka deti budú pracovať len s myškou, mačkou, husou, psom, kozou a baranom. Postupne pribúdajú úlohy na porovnanie síl v družstvách a menia sa aj otázky, ktoré deti dostávajú. V nasledujúcej úlohe (obr. 10) by sme sa mohli pýtať: Ktoré družstvo je silnejšie? Ktoré družstvo je slabšie? Aké zvieratko má prísť na pomoc slabšiemu družstvu, aby sa sily vyrovnali? Ktoré zvieratko má odísť zo silnejšieho družstva, aby sa sily vyrovnali? Môže silnejšie družstvo požičať zvieratko slabšiemu tak, aby sa ich sily vyrovnali? a podobne.
Neskôr sa objavia úlohy z maškarného bálu, zvieratká sa nám skryjú za masky (obr. 11) a pribúdajú úlohy: Zisti, aké zvieratko je pod maskou. Alebo pod maskami? (obr. 12)
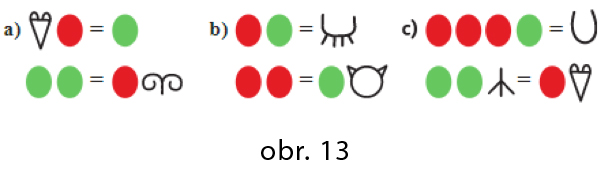
Nuž, nemajú to tie deti s nami ľahké! Ony sa rady hrajú a hrou toho naozaj veľa objavia. Okrem už spomínanej substitúcie sa pri odoberaní a pridávaní zvieratiek do oboch súperiacich družstiev zoznámia s ekvivalentnými úpravami a postupne sa zoznámia so všetkými spôsobmi riešenia lineárnych rovníc ako i sústav lineárnych rovníc. Zvieratká Deda Lesoňa postupne úplne prirodzene nahradia číslami, ktoré reprezentujú ich silu. A to úplne samy (v ideálnom prípade) bez našej pomoci. Samy zistia, že rovnicou x+x+x+2 = 10+5+2 môžu nahradiť 
vzťah a naopak, že pod rovnicou 3x+2 = 17 si vždy môžu predstaviť uvedené zvieratká Deda Lesoňa. Rovnako ako Krokovanie, Váhy, Myslím si číslo, Hady a ďalšie prostredia, ktoré našim deťom pomáhajú riešiť rovnice s pochopením a nie len mechanickým opakovaním operácií, ktorým nerozumejú. A čo vy dospeláci, trúfnete si vyriešiť sústavy rovníc Deda Lesoňa? Viete, aké zvieratká sa skrývajú za maskami? (obr. 13)
